It can be shown that

(1")     

The cross-sectional area of the conductor need not be circular or square. In general, the area can be expressed as:

(2")     

where:

A is the cross-sectional area,

C is a constant determined by the shape of the conductor (C=1 for square and C= p/4 for circular cross-sections), and

D is the transverse dimension (D=side length for a square and D=the diameter for circular cross-sections).

Introducing the general area equation into Equation 1" yields:

(3")     

It is convenient to introduce axial strain, lateral strain and Poisson's ratio. The axial strain, ea,is:

(4")     

where:

dL is the change in length of the conductor.

The lateral strain, et, is:

(5")     

where:

dD is the change in the transverse size of the conductor.

Poisson's ratio, 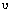, is defined as the ratio of lateral strain to axial strain:

(6")     

Rewriting Equation (3') and rearranging yields:

(7")     

Assuming constant properties, 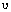is constant and d /is negligible. Let the gauge factor, F, be defined as the constant of proportionality between dR/R and a. F is found by dividing Equation 7" by Equation 4":

(8")     

Thus, rewriting Equation 8" taking into account constant properties, we have:

(9")     

the relationship that the change in resistance of a conductor is linearly related to the strain. Rearranging Equation 9" gives:

(2)